10. Sınıf Matematik Ders Kitabı Sayfa 37-39 Cevapları Meb Yayınları

10. Sınıf MEB Matematik Sayfa 37 – 9. Uygulama

Üçgenin İç Açıortaylarının Kesim Noktası Cevapları

Soru - Bir üçgenin iç açıortaylarının tek noktada kesişip kesişmediğini, kesişiyorsa bu noktanın özelliğini grup arkadaşlarınızla tartışınız. Uzlaştığınız fikirlerden yola çıkarak varsayımlarda bulununuz.

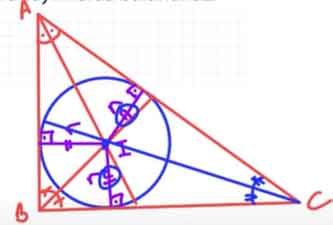
• Üçgenin iç açıortayları her zaman tek bir noktada kesişir.
• Bu nokta, üçgenin iç teğet çemberinin merkezidir.
• İç teğet çember, üçgenin kenarlarına teğet olan çemberdir.
• Bu kesişim noktası, üçgenin iç merkezi olarak adlandırılır.

10. Sınıf Matematik Ders Kitabı Sayfa 38 Cevapları (MEB Yayınları)

Soru 2: Bir üçgenin iç açıortaylarının tek noktada kesişip kesişmediğini ve kesişiyorsa bu noktanın özelliğine ulaşmak için yaptığınız varsayımları grup arkadaşlarınızla tartışarak genellemelerinizi oluşturunuz.

Cevap: Üçgenin iç açıortayları tek bir noktada kesişir. Bu nokta, üçgenin iç teğet çemberinin merkezidir. İç teğet çemberin merkezinden kenarlara inilen dikmeler eşit olduğundan, bu merkez aynı zamanda kenarlara eşit uzaklıkta bir noktadır.

Soru 3: Matematik yazılımlarını kullanarak verilen adımları gerçekleştiriniz ve soruları cevaplayınız.

a) Her durumda çember ile üçgenin ilişkisini inceleyerek değerlendirmenizi yazınız.

• Çember, üçgenin kenarlarına teğet olacak şekilde iç bölgesinde yer alır.
• Bu çember iç teğet çember olup merkez noktası iç açıortaylarının kesim noktasında bulunur.

b) Her durumda |KD|, |KE| ve |KF| arasındaki ilişkiyi inceleyip değerlendirmenizi yazınız.

|KD| = |KE| = |KF| eşitliği vardır. Yani merkezin kenarlara olan uzaklıkları birbirine eşittir.

c) Bir üçgenin iç bölgesinde olup üçgenin tüm kenarlarına teğet olan çembere ne ad verilir? Bu çemberin merkezi olan noktanın özelliklerini yazınız.

• Bu çembere iç teğet çember denir.
• İç teğet çemberin merkezi, iç açıortaylarının kesim noktasıdır.
• Bu merkez, üçgenin tüm kenarlarına eşit uzaklıktadır.

Soru 4: Oluşan her üçgen için 3. maddede elde ettiğiniz sonuçlardan hareketle genellemelerinizi varsayımlarınızla karşılaştırınız.

Cevap: Varsayımlarımız ile elde edilen sonuçlar örtüşmektedir. Yani:

• Üçgenin iç açıortayları tek noktada kesişir.
• Bu nokta, iç teğet çemberin merkezidir.
• Merkezin kenarlara uzaklığı eşittir.

Böylece, üçgenin iç açıortaylarının kesim noktası = iç teğet çemberinin merkezi olduğu sonucuna ulaşılır.

10. Sınıf MEB Matematik Ders Kitabı Sayfa 39 Cevapları

Soru 5: Elde ettiğiniz genellemelerden hareketle bir üçgenin iç açıortaylarının tek noktada kesişip kesişmediğini, kesişiyorsa bu noktanın özelliğine dair önermenizi ifade ediniz.

Cevap: Üçgenin iç açıortayları tek bir noktada kesişir. Bu nokta, üçgenin iç teğet çemberinin merkezidir.

Soru 6: Aşağıdaki haritada gösterilen caddenin her birinden eşit uzaklıkta olacak şekilde okul inşa edilmek isteniyor.

a) Haritada üç caddenin her birine eşit uzaklıkta olan noktanın özelliklerini belirtiniz.

Cevap: Bu nokta, üçgenin iç açıortaylarının kesim noktasıdır.

b) Haritayı iki farklı doğru parçasına göre katlayarak üç caddeye de eşit uzaklıkta olan noktayı bulma adımlarını yazınız.

1. Önce Dostluk Caddesi ile Barış Caddesi üst üste gelecek şekilde katlanır. Kat izi bir iç açıortaydır.
2. Daha sonra Sevgi Caddesi ile diğer caddelerden biri üst üste gelecek şekilde katlanır. Bu da ikinci iç açıortayı verir.
3. İki açıortayın kesişim noktası üç caddeye eşit uzaklıktaki noktadır.

Genelleme: Üçgenin iç açıortayları tek bir noktada kesişir ve bu nokta üçgenin iç teğet çemberinin merkezi olup kenarlara eşit uzaklıktadır.